March 16, 2018

HeapSort & Priority Queue 学习笔记

二项堆

二项堆（Binary Heap）指用线性数组所表示满二叉树（Complete Binary Tree）的一种数据结构。

若数组下标从 1 开始记，则有

若 parent 节点的下标为 N
则其 left child 的下标为 2N
right child 的下标为 2N+1

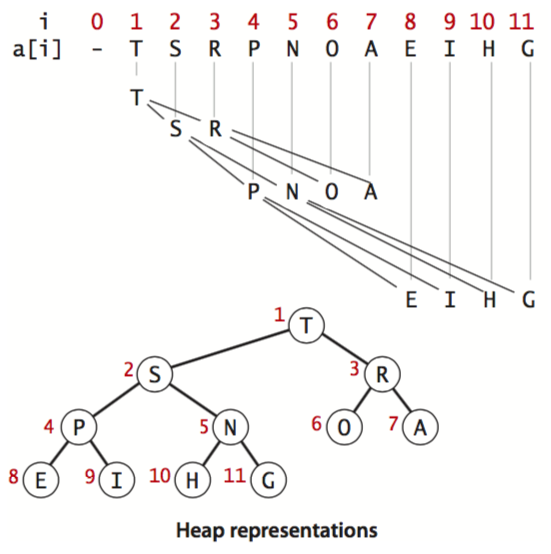
heap representations

约定 parent 节点不大于（或小于）子节点，则形成了一个部分有序的堆结构

堆排序

不同于其它排序算法，需要将整个输入序列完全排序。堆排序约束一个更宽松的规则：

子树的根结点不大于（或小于）其子结点

根结点为最大值的堆称为 MaxHeap，反之称为 MinHeap

当插入新的元素，或修改堆元素的顺序后，堆的规则被破坏，需要进行维护（reheapifying），其时间复杂度为 $O(\log(n))$ 。通过循环交换第一个元素到末尾，并重新维护前 N-1 个序列的堆排序，就实现了对整个输入的排序，时间复杂度为 $O(n\log(n))$

二项堆具有以下特性

大小为 N 的二项堆其高度为 $\lfloor \lg{N} \rfloor$
长度为 N 的数据，插入操作最多进行 $ 1+\lg{N} $ 次比较，移除最大值最多进行 $2 \lg{N}$ 次比较
堆排序 N 个元素，最多进行 $2N\lg{N} + 2N$ 次比较

heapify

当新加入结点，或改变结点的 key 大小（调整优先级），则破坏了堆的排序条件（heap condition）。需要通过 up 或 down 两个操作来维护堆条件。以 MaxHeap 为例（根结点为最大值）

Bottom-up reheapify (swim). 当插入或修改结点，使它的值大于 parent，则需要与 parent 互换。互换后在 parent 位置继续进行 swim 操作（递归），直到其不大于 parent 或回到了 root，如下图所示
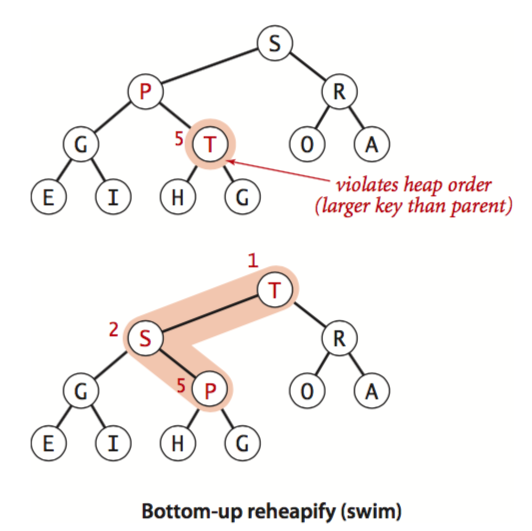
Top-down reheapify (sink). 当结点值变小，小于了任一个子结点，则需要递归方式下沉该节点，直到两个子结点均小于它，或到达叶子结点（没有子结点）。如下图所示

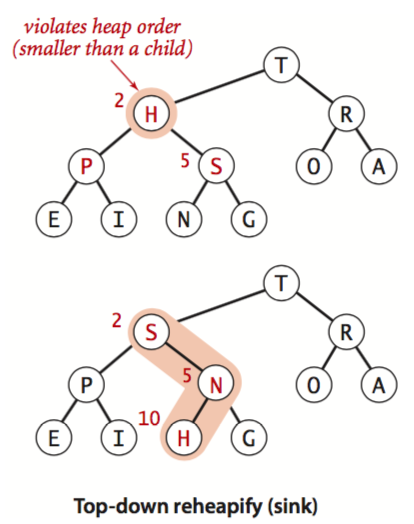
堆的两个基本操作正是基于 swim 和 sink 来实现的：

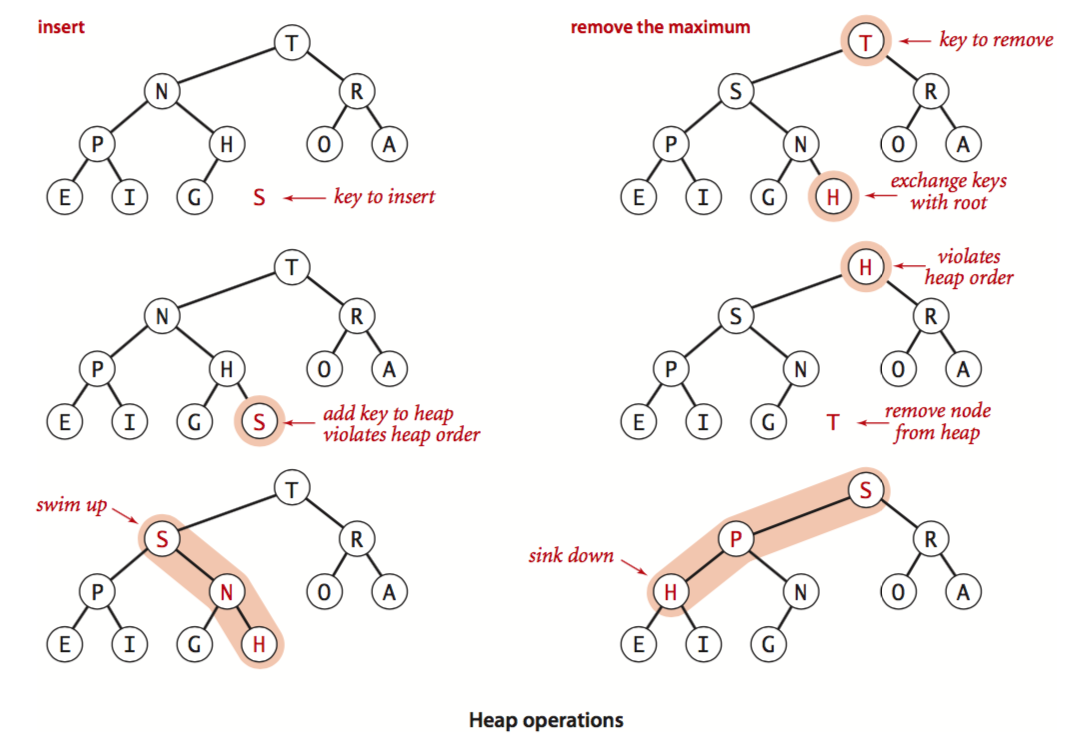
插入新结点。增大堆大小，插入结点到末尾，对其进行 swim 操作
删除最大值。将 root 与结尾元素互换，减小堆大小，对 root 进行 sink 操作

heap operations

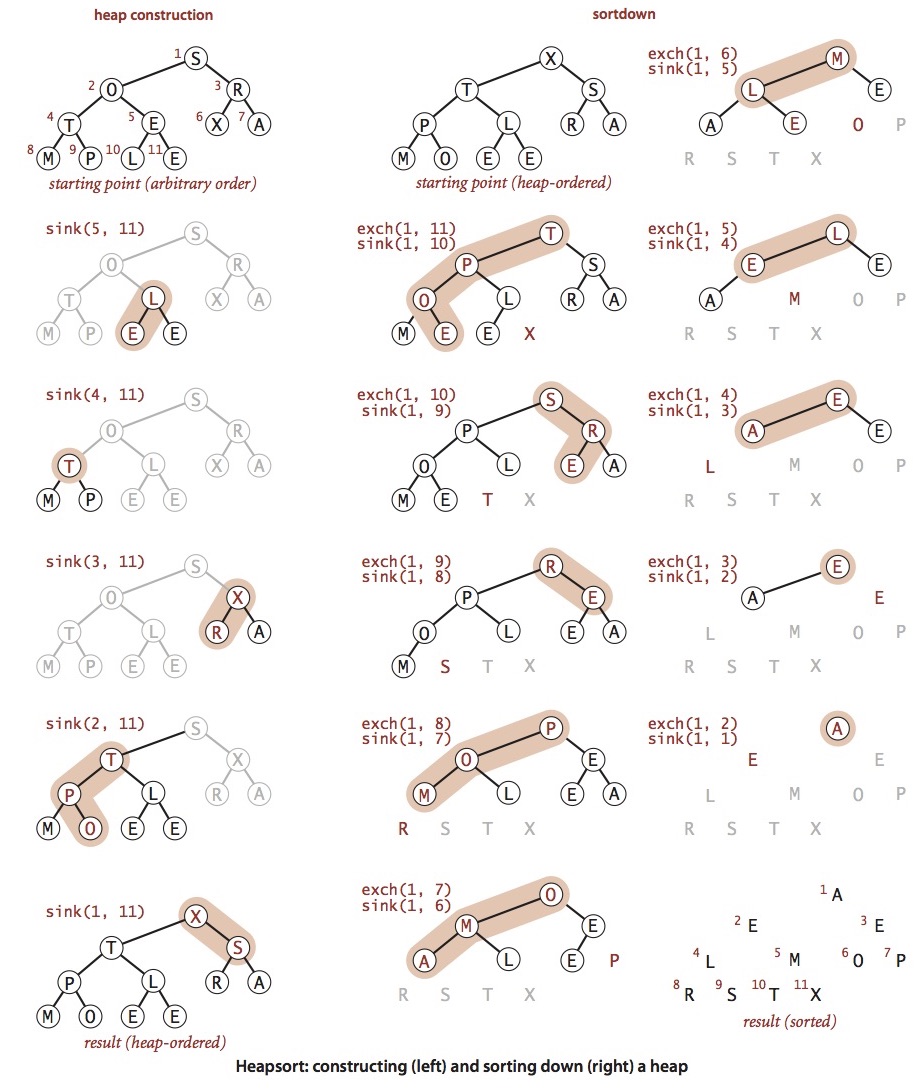
heapSort

堆排序分为两步

heap construction, 自右向左，始终保证 subnode 符合 heap condition
sortdown，移除首个元素（通过与最后一个元素交换，并减少堆长度，对 root 进行 sink 维护）

heap-sort

优化思路

MultiWay Heap，可以将二项堆变成三项或更多，这样可以减少树的调试，但在 sink 时会因为子结点变多而效率相对变低
底层数组可以考虑动态扩展大小，不必在初始化时申请好固定大小
只允许增加或删除，而不允许修改

优先队列

优先级队列（priority queue）与堆排序算法密切相关。

因为可以取出其中第一个最大（或最小）的元素，常用于实现以下功能：

操作系统进程按优先级调用，每次取出最高优先级进程，并可以插入新的进程，或修改旧的进程优先级
模拟事件请求，按时间顺序触发回调
取无限序列的前 M 个最大值（或最小值）
使用 Multiway Heap 技术，可以实现多路流数据的 merge 操作

优先级队列除了堆实现外，还有一些朴素的方式来实现，如

选择排序思路，每次扫描全表，找出其中最大的元素
插入排序思路，写入时插入到合适的顺序，保证最大元素总在最后

但这些方式，或查询时间复杂度为 O(n)，或插入时间复杂度为 O(n)。相比于堆排序的 O(log(n)) 在大输入量下劣势明显

go `container/heap` 实现

go 标准库中有 heap 的实现，

其中定义 heap 为 MinHeap，最小值位于 root。如果要实现 MaxHeap，则需要反转 Less效果即可
不同于书中使用 1 作为 root 下标，go 中使用 0 作为下标，这样结点 k 的左子为 2k+1, 右子为 2k+2，父结点为 (k-1)/2
优先级队列使用，提供了 Push 和 Pop方法，相当于 Insert 和 DelMin（因为 Less 反转相当于 DelMax）

Heap 底层与 Sort 一致，需要提供 Less, Len, Swap 三个方法，除此之外，需要向底层中添加新的元素或删除元素(与 Heap 的 Push 和 Pop 不同，是算法实现需要调用的接口方法)

type Interface interface {
	sort.Interface		//- embedded Interface sort.Interface
	Push(x interface{}) // add x as element Len()
	Pop() interface{}   // remove and return element Len() - 1.
}

Heap Construction 由 Init 函数实现，与书中建议的方式一样，从右向左（忽略 $[n/2, N)$，因为其为叶子结点）添加元素，并作 sink（down）操作以维护 heap condition

func Init(h Interface) {
	// heapify
	n := h.Len()
	for i := n/2 - 1; i >= 0; i-- {
		down(h, i, n)
	}
}

Push 操作插入新元素到结尾，并作 swim（up）维护

func Push(h Interface, x interface{}) {
	h.Push(x)
	up(h, h.Len()-1)
}

Pop 和 Remove 操作，将元素与末尾交换，减小 heap size，并对当前位置作 sink 维护

func Pop(h Interface) interface{} {
	n := h.Len() - 1
	h.Swap(0, n)
	down(h, 0, n)
	return h.Pop()
}

func Remove(h Interface, i int) interface{} {
	n := h.Len() - 1
	if n != i {
		h.Swap(i, n)
		if !down(h, i, n) {
			up(h, i)
		}
	}
	return h.Pop()
}

当修改了一个元素的大小，需要对该位置进行维护，但我们事先不知道其是增大或是减少。若增大，则需要 down 操作，否则则需要 up。Go 中的实现，为 down 添加一个 bool 的返回值，如果进行了下沉操作则返回 true。对一个元素的维护，只能是下沉或上浮中的一种，不会同时出现。

func Fix(h Interface, i int) {
	if !down(h, i, h.Len()) {	//- down 需要指定长度，因为要判定是否达到子结点
        up(h, i)	//- up 不需要指定长度，因为最多回到 root (0)
	}
}

func up(h Interface, j int) {
	for {
		i := (j - 1) / 2 // parent
		if i == j || !h.Less(j, i) {	// 如果 ai <= aj，即父结点更小或相等，则不需要交换
			break
		}
		h.Swap(i, j)
		j = i
	}
}

func down(h Interface, i0, n int) bool {
	i := i0
	for {
		j1 := 2*i + 1
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
			break
		}
		j := j1 // left child
		if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
			j = j2 // = 2*i + 2  // right child
		}	//- j 指向最大的那个子结点
		if !h.Less(j, i) {	// 如果 aj >= ai，即子结点大于或等于当前节点，则不需要交换
			break
		}
		h.Swap(i, j)
		i = j
	}
	return i > i0	// 是否发生交换
}

性能

Go 代码中列出了各个操作的时间复杂度，摘录如下

方法	时间复杂度
Init	$O(N)$ why?
Push	$O(\lg{N})$
Pop	$O(\lg{N})$
Remove	$O(\lg{N})$
Fix	$O(\lg{N})$
Up	$O(\lg{N})$
Down	$O(\lg{N})$

例子

取出最大的 N 行数据

package main

import (
	"bufio"
	"container/heap"
	"fmt"
	"os"
	"strings"
)

type stringHeap []string

func (s stringHeap) Len() int {
	return len(s)
}

func (s stringHeap) Less(i int, j int) bool {
	return strings.Compare(s[i], s[j]) < 0
}

func (s stringHeap) Swap(i int, j int) {
	s[i], s[j] = s[j], s[i]
}

func (s *stringHeap) Push(x interface{}) {
	(*s) = append(*s, x.(string))
}

func (s *stringHeap) Pop() (v interface{}) {
	v, (*s) = (*s)[len(*s)-1], (*s)[:len(*s)-1]
	return
}

const max = 10

func main() {
	h := &stringHeap{}
	heap.Init(h)
	for _, args := range os.Args[1:] {
		file, err := os.Open(args)
		if err != nil {
			panic(err)
		}

		buf := bufio.NewScanner(file)
		for buf.Scan() {
			line := buf.Text()
            heap.Push(h, line)	// 千万注意，这里用的是 heap.Push(h,line)，而不是 h.Push(line)
			if h.Len() > max {
				heap.Pop(h)
			}
		}

	}

	for h.Len() > 0 {
		fmt.Println(heap.Pop(h))
	}
}

参考资料

Algorithm 4th Edition, 2.4 Priority Queues